Хэш-функции — невероятно красивые математические объекты. Они могут отображать произвольные данные на небольшую область выходных данных фиксированного размера таким образом, что отображение оказывается детерминированным, хоть и кажется случайным. Такая «детерминированная случайность» невероятно полезна для широкого спектра применений, например, для хэш-таблиц, контрольных сумм, алгоритмов Монте-Карло, распределённых алгоритмов без коммуникаций и так далее.
В этой статье мы взглянем на тёмную сторону хэш-функций: ситуации, когда всё идёт не так. К счастью, такое, по сути, в реальной жизни никогда не происходит из-за неудачных входных данных (по крайней мере, в случае хороших хэш-функций). Однако кроме программ существуют и люди, и не все из них настроены миролюбиво, поэтому нам следует обратиться за ответами к сфере компьютерной безопасности. Я вкратце объясню основы безопасности хэш-функций, а затем покажу, насколько легко поломать эту безопасность для некоторых популярных некриптографических хэш-фукнкций.
Для затравки скажу, что в этой статье объясняется, как генерировать за секунду тысячи подобных строк:
Также я покажу, как можно создавать очень специфичные пары строк, которые можно произвольно конкатенировать таким образом, что при конкатенации k строк любая из 2k комбинаций будет иметь одинаковый хэш вне зависимости от использованного для хэш-функции порождающего значения (seed):
murmurhash3(a + a, seed) == murmurhash3(b + b, seed)
Если хэш-функция не ведёт себя случайным образом, то мы можем взломать описанные выше конструкции безопасности. Поэтому в криптографических хэш-функциях аспект случайности воспринимается крайне серьёзно. Идеальная хэш-функция должна выбирать свой результат совершенно случайно для каждых входных данных, запоминая этот выбор для будущих вызовов. Это называется случайным оракулом.
Проблема заключается в том, что случайный оракул требует истинного генератора случайных чисел и, что более проблематично, доступного из любой точки мира бесконечного банка памяти. Поэтому мы аппроксимируем его при помощи детерминированных хэш-функций. Они вычисляют свои выходные данные, по сути, очень хорошо «перетасовывая» свои входные данные таким образом, что их невозможно обратить.
Для вычисления меры того, насколько хорошо конкретная функция приближается к случайному оракулу, криптографы придумали различные свойства, которыми должен обладать случайный оракул. Вот три самых важных и известных свойств, которым должна удовлетворять безопасная криптографическая хэш-функция:
В общем случае мы считаем, что одно из этих свойство сломано, если существует способ создания коллизии или прообраза быстрее, чем перебор случайных входных данных (также называемый атакой перебором, brute force attack). Однако существуют градации ломаемости, поскольку некоторые способы лишь на несколько порядков величин быстрее, чем перебор. Это может показаться серьёзным, но даже если способ требует 2110 шагов вместо 2128, то оба способа всё равно невозможно реализовать на мощностях современных компьютеров.
Раньше распространённой хэш-функцией была MD5, а SHA-1 активно используется и сегодня. Хотя обе они когда-то считались криптографически безопасными, сегодня для генерации коллизий MD5 на современном компьютере требуется меньше секунды. В 2017 году группа исследователей из CWI и Google объявила об открытии первой коллизии SHA-1. Однако, насколько я знаю, ни MD5, ни SHA-1 не имеют практических атак нахождения первого и второго прообраза, только теоретические.
Один из сценариев использования хэш-функций — генерация секретного ключа на основе пароля: функция формирования ключа. В отличие от обычных хэш-функций, здесь низкая скорость на самом деле становится мерой безопасности для защиты от перебора паролей. Современные функции наподобие Argon2 также намеренно используют много памяти, чтобы защититься от специализированного оборудования, например, ASIC или FPGA.
Для многих задач использование безопасных хэш-функций необязательно, и люди часто предпочитают повышенную скорость хэширования, особенно когда нужно вычислять множество мелких хэшей, например, в хэш-таблице. Давайте узнаем, что популярные реализации хэш-функций используют в качестве хэша для строк:
Большинство операций с целочисленными регистрами тоже обратимо, несмотря на то, что в случае переполнения целые числа делятся с остатком на 2w. Давайте рассмотрим несколько операций:
Сложение можно обратить при помощи вычитания. То есть x += y можно обратить при помощи x -= y. Всё достаточно очевидно.
Умножение на константу c не обратимо делением. Оно не сработает в случае переполнения. Вместо этого мы вычисляем обратное по модулю число для c. Это такое целое c−1, что c⋅c−1≡1(modm). Таким образом, можно обратить умножение на c, просто умножив на c−1.
Эта константа существует тогда и только тогда, когда c является взаимно простым с делителем m; для нас это означает, что c должно быть нечётным, поскольку m=2n. Например, умножение на 2 необратимо, поскольку это эквивалент битового сдвига влево на одну позицию с потерей навсегда старшего бита.
Не особо вдаваясь в подробности, приведу код на Python, вычисляющий обратное по модулю число для целого при помощи расширенного алгоритма Евклида, вычисляющего такие x,y, что
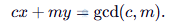
Тогда поскольку c взаимно простое, мы находим gcd(c,m)=1 (gcd — это наибольший общий делитель), и это означает, что

то есть x=c−1.
При помощи этого кода мы можем обратить умножение по модулю:
Магия!
XOR можно обратить при помощи … XOR. Это обратная самой себе операция. То есть x ^= y можно обратить при помощи x ^= y.
Битовые сдвиги обратить невозможно, но две часто используемые в хэш-функциях операции, задействующие битовые сдвиги, обратить можно. Первая — это циклический сдвиг (bit rotation) на константу. Лучше всего это объяснить наглядно, например, циклический сдвиг 8-битного слова влево на три позиции, в котором каждый бит обозначен буквой:
Формула циклического сдвига вправо на k позиций имеет вид (x >> k) | (x << (w - k)), где w — ширина целочисленного типа. Обратная ему операция — это циклический сдвиг влево, который просто меняет направление обоих сдвигов. Или же обратной для операции циклического сдвига вправо на k позиций будет ещё один циклический сдвиг вправо на w-k позиций.
Ещё одна часто используемая в хэш-функциях операция — это xorshift. Это операция одного из двух типов, где k>0:
Их способ обращения полностью аналогичен, поэтому я рассмотрю левый xorshift.
Здесь важно отметить, что на младшие k битов xorshift совершенно не влияет. Таким образом, повторяя операцию, мы восстановим младшие 2k битов, так как XOR обратит себя для следующих k битов. Давайте взглянем на полученное значение, чтобы понять, как действовать дальше:
Из этого можно вывести следующее равенство:

Теперь, чтобы алгоритм стал завершённым, нам нужно ещё одно наблюдение: xorshift для k≥w, где w — это ширина целого числа, является no-op. Таким образом, мы многократно применяем удваивающее равенство, пока не достигнем такого достаточно большого q, что xorshift(x,2q⋅k)=x.
Например, чтобы обратить левый xorshift на 13 для 64-битных целых чисел, нам нужно выполнить следующий порядок действий:
Вооружившись этим знанием, мы можем приступать к атакам.
Код стандартной библиотеки C++ подвергается процессу «обезображивания» (uglification), добавляющему перед всеми идентификаторами нижние подчёркивания. Это вызвано тем, что такие идентификаторы зарезервированы стандартом для использования в стандартной библиотеке, а потому не будут заменяться макросами из соблюдающего стандарт кода. Заботясь о вашем душевном здоровье, я убрал их из кода.
Чтобы поломать этот код, допустим, что мы всегда передаём входные данные длиной 32. Тогда реализация всегда будет вызывать hash_len_17_to_32, а мы будем иметь полный контроль над a, b, c и d при помощи изменения входных данных.
Обратите внимание, что d используется только один раз, в последнем выражении, поэтому становится основной целью для атаки на хэш. Мы выберем a, b и c произвольно, а затем решим уравнение для переменной d, чтобы вычислить желаемый хэш.
При помощи показанной выше функции modinv мы сначала вычисляем нужные обратные по модулю числа для mul и k0:
Также отметим, что в этом случае xorshift легко обратить, поскольку x ^= x >> 47 является всего лишь обратным самому себе. Подготовив все компоненты, мы можем поэтапно обратить функцию.
Сначала мы загружаем a, b и c, как в хэш-функцию, и вычисляем
то есть второй параметр hash_len_16. Затем начиная с нашего желаемого возвращаемого значения hash_len_16(u, v) мы пошагово движемся обратно, обращая каждую операцию для нахождения аргумента функции u, который даст нам целевой hash. Когда мы найдём такое уникальное u, то вычислим требуемое входное d. Соединим всё вместе:
Вероятность того, что случайное uint64_t образует 8 печатаемых байтов ASCII, равна (94/256)8 ≈ 0,033. Не очень здорово, но cityhash64_preimage32 настолько быстра, что необходимость повторить её примерно три тысячи раз для получения результата из чистого ASCII — это не так уж плохо.
Например, все следующие 10 строк хэшируются в 1337 при использовании CityHash64, сгенерированного при помощи этого кода:
Я заметил, что реальном использовании существуют варианты CityHash64 с незначительными различиями. Я решил атаковать вариант в комплекте libc++, поэтому это должно сработать, например, для её std::hash. Также в статье мы будем рассматривать машину little-endian, на машине big-endian в зависимости от реализации кэша ситуация может быть другой.
Здесь мы можем использовать ту же методику, что и раньше. Заметим, что обратное по модулю число для 0xc6a4a7935bd1e995 mod 264 — это 0x5f7a0ea7e59b19bd. В качестве примера мы можем выбрать первые 24 байта произвольным образом и найти решение для последних 8 байтов:
Все десять показанных ниже строк хэшируются в этом коде при помощи MurmurHash64A с стандартным seed 0xc70f6907 в 1337:
Что же касается CityHash64, то для него они тоже нашли универсальные коллизии вне зависимости от используемого seed. На самом деле, CityHash64 поломать таким образом гораздо проще, поскольку простая представленная выше атака нахождения прообраза, нацеленная на 0 в качестве хэша, делает выходные данные полностью зависимыми от seed, а значит, создаёт универсальную коллизию.
Чтобы понять, как это работает, давайте взглянем на основной цикл MurmurHash64A:
Мы знаем, что тривиальным образом можем обратить выполняемые с data операции вне зависимости от текущего состояния, поэтому вполне могли бы иметь следующее тело:
Теперь хэш и в самом деле начинает выглядеть довольно слабо. Авторы исследования использовали хитрый трюк: создавали одновременно две строки так, чтобы они отличались ровно на старший бит в каждом 8-байтном слове. Почему на старший бит?
Так как mul нечётное, самый младший бит установлен. Умножение 1 << 63 на него эквивалентно сдвигу этого бита на 63 позиций влево, что снова будет равно 1 << 63. То есть 1 << 63 — это фиксированная точка для операции state *= mul. Также стоит отметить, что XOR старшего бита эквивалентно сложению, поскольку переполнение от сложения убирается mod 264.
То есть если у нас есть две входные строки: одна, начинающаяся с 8-байтных data, а другая, начинающаяся с data ^ (1 << 63) == data + (1 << 63) (после выполнения тривиальных инверсий) — то мы выясним, что два состояния вне зависимости от seed различаются ровно на старший бит после state ^= data. После умножения мы обнаружим, что два состояния имеют вид x * mul и (x + (1 << 63)) * mul == x * mul + (1 << 63)… то есть снова различаются ровно на верхний бит! Теперь мы вернулись для следующих 8 байтов к state ^= data в нашей итерации. Можно воспользоваться этим моментом для отмены разницы в старшем бите, снова передав две 8-байтные строки, отличающиеся на старший бит (после обращения).
На самом деле, нам достаточно найти только одну пару таких строк, отличающихся на старший бит, которую мы затем можем повторить дважды (в любом порядке), чтобы снова отменить разницу. Если данные представлены в виде uint64_t, то когда мы выберем первую строку как x, сможем получить вторую строку как
Мне не удалось найти печатаемую строку ASCII, которая бы имела в качестве пары другую печатаемую строку ASCII. Но я нашёл следующую пару 8-байтных строк UTF-8, после преобразования входных данных Murmurhash64A отличающуюся ровно на верхний бит:
Скомбинировав их, мы получим две 16-байтные строки, которые при обработке алгоритмом хэширования позволяют манипулировать состоянием аналогичным образом: создавая коллизию.
Но на этом всё не заканчивается. Выполнив конкатенацию этих двух строк, мы можем создать 2n различных строк с коллизиями, каждая из которых имеет длину 16n. При текущей реализации libstdc++ показанный ниже код выведет восемь раз одно и то же число:
Даже если бы libstdc++ рандомизировала seed, используемый MurmurHash64a, коллизии строк всё равно бы происходили.
использует раньше использовал MurmurHash3_x86_32, поэтому давайте попробуем поломать его.
Пока я прокрастинировал, заканчивая эту статью, Nim перешёл на использование farmhash. Сделайте вид, что он всё ещё использует MurmurHash3, чтобы мои слова имели смысл. А потом я поломаю и farmhash.
Если мы снова упростим и будем учитывать только строки, длина которых кратна 4, то получим следующий код:
Думаю, теперь вы уже должны понимать, как заставить эту функцию выдавать любые значения, если знаете seed. Инверсией rotl32(x, r) будет rotl32(x, 32-r), а инверсией h ^= h >> 16 снова будет просто h ^= h >> 16. Только с h ^= h >> 13 ситуация немного отличается: мы впервые видим здесь, что инверсия xorshift требует больше, чем один шаг:
Вычислим обратные по модулю числа для значений с c1 по c4, а также 5 mod 232. Если вы хотите сжульничать или проверить свой ответ, то можете заглянуть в код , который я использовал для генерации следующих десяти строк, которые при передаче MurmurHash3_x86_32 с seed 0 все хэшируются в 1337:
Nim использует в качестве фиксированного seed 0.
Вы можете задаться вопросом этичности публикации функций для генерации произвольного количества коллизий для хэш-функций, которые продолжают использоваться сегодня. Но атака HashDoS известна уже почти два десятка лет, а показанные мной универсальные коллизии хэшей, тоже были опубликованы больше десятка лет назад. У всех желающих было достаточно времени, чтобы всё исправить.
Да, можем. Давайте ещё раз взглянем на тело основного цикла:
Можно снова игнорировать первые три тривиально обратимые команды, потому что мы можем просто выбрать входные данные так, чтобы получить нужное нам k. Вспомним из предыдущего примера, что мы хотим добавить разницу только в старший бит h, так как при умножении эта разница сохранится. Но между XOR и умножением присутствует циклический битовый сдвиг. Как же решить эту проблему? Просто вставить нашу разницу битов так, чтобы rotl32(h, 13) сдвигал её в старшую позицию.
Помешает ли нам прибавление 0xe6546b64? Нет. Поскольку между двумя состояниями различается только старший бит, между двумя состояниями существует разность, равная 231. Эта разность сохраняется при сложении. Так как два 32-битных числа с одинаковым старшим битом могут быть иметь расстояние между друг другом не более 231−1, можно сделать вывод, что после сложения два состояния по-прежнему будут различаться в старшем бите.
То есть мы хотим найти две пары 32-битных int, такие, что после применения первых трёх команд первая пара будет отличаться в бите 1 << (31 - 13) == 0x00040000, а вторая — в бите 1 << 31 == 0x80000000.
После поиска перебором я нашёл несколько хороших пар (мне снова пришлось использовать UTF-8), которые при комбинировании дали мне следующую коллизию:
Как и раньше, любая конкатенация строк a и b длиной n образует коллизию со всеми комбинациями длиной n.
Для протокола: это не претензия к wyhash в целом. Он кажется надёжным, если используется с секретным рандомизированным seed. Я просто хочу показать, что если использовать его с фиксированным seed, то он тривиально ломается.
Здесь можно легко увидеть критичный недостаток: если одна из половин равна нулю, то результатом тоже будет ноль. Чтобы защититься от этого, wyhash всегда использует folded multiply в следующем виде:
где secret_a и secret_b определяются по seed или по выходным данным предыдущих итераций, на которые влиял seed. Однако когда seed константа… Применив немного изобретательности , мы можем использовать начало нашей строки для подготовки «секретного» значения, которое мы можем прекрасно обнулить с другой строкой ASCII в дальнейшем во входных данных.
Итак, без лишних предисловий скажем, что каждая 32-битная строка вида
хэшируется хэшером Zig по умолчанию в одно и то же значение.
Zig использует набор параметров, отличающийся от значений по умолчанию из репозитория wyhash, поэтому надо добавить, что этот паттерн обеспечивает произвольные множественные коллизии для параметров по умолчанию, найденных в wyhash, и при использовании seed == 0:
Также мы увидели, что некоторые хэш-функции уязвимы к атаке даже при случайных seed. Они полностью сломаны и их нельзя использовать, если существует хотя б минимальная возможность атаки. К счастью, мне не удалось найти такие атаки против большинства хэшей, но возможность ее существования пугает.
При использовании универсального хэширования можно создать хэш-функции, но такая атака доказуемо невозможна: в прошлом году я опубликовал хэш-функцию polymur-hash, обладающую таким свойством. Кроме того, ваше HTTPS-подключение к моему веб-сайту, скорее всего, использует универсальную хэш-функцию для обеспечения подлинности передаваемых данных: и Poly1305, и GCM основаны на универсальном хэшировании для доказательства их безопасности.
Примечание: доказано, что такие атаки невозможны для неинтерактивных нападающих, но всё снова идёт прахом, если нападающий может изучать выходные хэши и использовать их, чтобы попытаться угадать ваш секретный ключ.
Разумеется, если ваши данные не контролируются пользователем или если отсутствует разумная модель безопасности в тех местах, где ваше приложение может подвергаться атакам, то вы можете обойтись более быстрыми и небезопасными хэшами.
В этой статье мы взглянем на тёмную сторону хэш-функций: ситуации, когда всё идёт не так. К счастью, такое, по сути, в реальной жизни никогда не происходит из-за неудачных входных данных (по крайней мере, в случае хороших хэш-функций). Однако кроме программ существуют и люди, и не все из них настроены миролюбиво, поэтому нам следует обратиться за ответами к сфере компьютерной безопасности. Я вкратце объясню основы безопасности хэш-функций, а затем покажу, насколько легко поломать эту безопасность для некоторых популярных некриптографических хэш-фукнкций.
Для затравки скажу, что в этой статье объясняется, как генерировать за секунду тысячи подобных строк:
Код:
cityhash64("orlp-cityhash64-D-:K5yx*zkgaaaaa") == 1337
murmurhash2("orlp-murmurhash64-bkiaaa&JInaNcZ") == 1337
murmurhash3("orlp-murmurhash3_x86_32-haaaPa*+") == 1337
farmhash64("orlp-farmhash64-/v^CqdPvziuheaaa") == 1337Также я покажу, как можно создавать очень специфичные пары строк, которые можно произвольно конкатенировать таким образом, что при конкатенации k строк любая из 2k комбинаций будет иметь одинаковый хэш вне зависимости от использованного для хэш-функции порождающего значения (seed):
Код:
a = "xx0rlpx!xxsXъВ"
b = "xxsXъВxx0rlpx!"
murmurhash2(a + a, seed) == murmurhash2(a + b, seed)
murmurhash2(a + a, seed) == murmurhash2(b + a, seed)
murmurhash2(a + a, seed) == murmurhash2(b + b, seed)
a = "!&orlpՓ"
b = "yǏglp$X"
murmurhash3(a + a, seed) == murmurhash3(a + b, seed)
murmurhash3(a + a, seed) == murmurhash3(b + a, seed)Основы безопасности хэш-функций
Хэш-функции играют критическую роль в компьютерной безопасности. Они используются не только для верификации сообщений по защищённым каналам, но и для идентификации обновлений из доверенных источников, а также известных вирусов. Практически любая схема сигнатур начинается с хэш-функции.Если хэш-функция не ведёт себя случайным образом, то мы можем взломать описанные выше конструкции безопасности. Поэтому в криптографических хэш-функциях аспект случайности воспринимается крайне серьёзно. Идеальная хэш-функция должна выбирать свой результат совершенно случайно для каждых входных данных, запоминая этот выбор для будущих вызовов. Это называется случайным оракулом.
Проблема заключается в том, что случайный оракул требует истинного генератора случайных чисел и, что более проблематично, доступного из любой точки мира бесконечного банка памяти. Поэтому мы аппроксимируем его при помощи детерминированных хэш-функций. Они вычисляют свои выходные данные, по сути, очень хорошо «перетасовывая» свои входные данные таким образом, что их невозможно обратить.
Для вычисления меры того, насколько хорошо конкретная функция приближается к случайному оракулу, криптографы придумали различные свойства, которыми должен обладать случайный оракул. Вот три самых важных и известных свойств, которым должна удовлетворять безопасная криптографическая хэш-функция:
- Устойчивость к нахождению первого прообраза. Для константы c должно быть сложно найти такие входные данные m, что h(m)=c.
- Устойчивость к нахождению второго прообраза. Для входных данных m1 должно быть сложно найти другие входные данные m2, при которых h(m1)=h(m2).
- Устойчивость к коллизиям. Должно быть сложно найти такие входные данные m1,m2, что h(m1)=h(m2).
В общем случае мы считаем, что одно из этих свойство сломано, если существует способ создания коллизии или прообраза быстрее, чем перебор случайных входных данных (также называемый атакой перебором, brute force attack). Однако существуют градации ломаемости, поскольку некоторые способы лишь на несколько порядков величин быстрее, чем перебор. Это может показаться серьёзным, но даже если способ требует 2110 шагов вместо 2128, то оба способа всё равно невозможно реализовать на мощностях современных компьютеров.
Раньше распространённой хэш-функцией была MD5, а SHA-1 активно используется и сегодня. Хотя обе они когда-то считались криптографически безопасными, сегодня для генерации коллизий MD5 на современном компьютере требуется меньше секунды. В 2017 году группа исследователей из CWI и Google объявила об открытии первой коллизии SHA-1. Однако, насколько я знаю, ни MD5, ни SHA-1 не имеют практических атак нахождения первого и второго прообраза, только теоретические.
Некриптографические хэш-функции
Криптографически безопасные хэш-функции обычно имеют небольшую проблему: они медленные. Современные хэш-функции наподобие BLAKE3 частично решают её активной векторизацией хэша при помощи команд SIMD, а также распараллеливанием на несколько потоков, но для достижения таких скоростей им всё равно требуются большие объёмы входных данных.Один из сценариев использования хэш-функций — генерация секретного ключа на основе пароля: функция формирования ключа. В отличие от обычных хэш-функций, здесь низкая скорость на самом деле становится мерой безопасности для защиты от перебора паролей. Современные функции наподобие Argon2 также намеренно используют много памяти, чтобы защититься от специализированного оборудования, например, ASIC или FPGA.
Для многих задач использование безопасных хэш-функций необязательно, и люди часто предпочитают повышенную скорость хэширования, особенно когда нужно вычислять множество мелких хэшей, например, в хэш-таблице. Давайте узнаем, что популярные реализации хэш-функций используют в качестве хэша для строк:
- C++: существует множество реализаций стандартной библиотеки; в 64-битном clang 13.0.0 на Apple M1 применяется CityHash64. В настоящее время в libstdc++ применяется MurmurHash64A — разновидность Murmur2 для 64-битных платформ.
- Java: OpenJDK использует невероятно простой хэш-алгоритм, который, по сути, просто вычисляет h = 31 * h + c для каждого символа c.
- PHP: движок Zend, по сути, использует тот же алгоритм, что и Java, но с беззнаковыми integer и 33 в качестве множителя.
- Nim: раньше он использовал MurmurHash3_x86_32. Похоже, на момент написания статьи по умолчанию применяется farmhash.
- Zig: по умолчанию использует wyhash с 0 в качестве seed.
- Javascript: в V8 используется специализированный слабый строковый хэш со случайно инициализируемым seed.
- Если на x86-64 доступно аппаратное ускорение, в Go используется хэш на основе AES. Хоть он создаётся специализированным образом и, вероятно, не имеет полной криптографической безопасности, для его поломки потребуется слишком много усилий и, скорее всего, знания, которых у меня нет.
Если ускорение недоступно, то применяется алгоритм, источником вдохновения для создания которого стал wyhash. - В Python и Rust по умолчанию используется SipHash — криптографически безопасная псевдослучайная функция. По сути, это хэш-функция, в которой допускается использовать во время хэширования секретный ключ, в отличие от хэшей наподобие SHA-2, где все знают всю используемую информацию.
Интерлюдия: инвертирование операций
Прежде чем мы приступим к взлому некоторых из приведённых выше хэш-функций, я должен объяснить базовую методику, которую буду часто использовать: инвертирование операций. Впервые мы познакомились с ним в младшей школе, где нам давали задачи вида 2+x=10. Так мы узнали, что вычитание — это операция, обратная сложению, то есть мы можем найти x, вычислив 10−2=8.Большинство операций с целочисленными регистрами тоже обратимо, несмотря на то, что в случае переполнения целые числа делятся с остатком на 2w. Давайте рассмотрим несколько операций:
Сложение можно обратить при помощи вычитания. То есть x += y можно обратить при помощи x -= y. Всё достаточно очевидно.
Умножение на константу c не обратимо делением. Оно не сработает в случае переполнения. Вместо этого мы вычисляем обратное по модулю число для c. Это такое целое c−1, что c⋅c−1≡1(modm). Таким образом, можно обратить умножение на c, просто умножив на c−1.
Эта константа существует тогда и только тогда, когда c является взаимно простым с делителем m; для нас это означает, что c должно быть нечётным, поскольку m=2n. Например, умножение на 2 необратимо, поскольку это эквивалент битового сдвига влево на одну позицию с потерей навсегда старшего бита.
Не особо вдаваясь в подробности, приведу код на Python, вычисляющий обратное по модулю число для целого при помощи расширенного алгоритма Евклида, вычисляющего такие x,y, что
Тогда поскольку c взаимно простое, мы находим gcd(c,m)=1 (gcd — это наибольший общий делитель), и это означает, что
то есть x=c−1.
Код:
def egcd(a, b):
if a == 0: return (b, 0, 1)
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(c, m):
g, x, y = egcd(c, m)
assert g == 1, "c, m must be coprime"
return x % mПри помощи этого кода мы можем обратить умножение по модулю:
Код:
>>> modinv(17, 2**32)
4042322161
>>> 42 * 17 * 4042322161 % 2**32
42Магия!
XOR можно обратить при помощи … XOR. Это обратная самой себе операция. То есть x ^= y можно обратить при помощи x ^= y.
Битовые сдвиги обратить невозможно, но две часто используемые в хэш-функциях операции, задействующие битовые сдвиги, обратить можно. Первая — это циклический сдвиг (bit rotation) на константу. Лучше всего это объяснить наглядно, например, циклический сдвиг 8-битного слова влево на три позиции, в котором каждый бит обозначен буквой:
Код:
abcdefghi
defghiabcФормула циклического сдвига вправо на k позиций имеет вид (x >> k) | (x << (w - k)), где w — ширина целочисленного типа. Обратная ему операция — это циклический сдвиг влево, который просто меняет направление обоих сдвигов. Или же обратной для операции циклического сдвига вправо на k позиций будет ещё один циклический сдвиг вправо на w-k позиций.
Ещё одна часто используемая в хэш-функциях операция — это xorshift. Это операция одного из двух типов, где k>0:
Код:
x ^= x << k // Левый xorshift.
x ^= x >> k // Правый xorshift.Их способ обращения полностью аналогичен, поэтому я рассмотрю левый xorshift.
Здесь важно отметить, что на младшие k битов xorshift совершенно не влияет. Таким образом, повторяя операцию, мы восстановим младшие 2k битов, так как XOR обратит себя для следующих k битов. Давайте взглянем на полученное значение, чтобы понять, как действовать дальше:
Код:
v0 = (x << k) ^ x
// Применяем первый шаг инвертирования v1 = v0 ^ (v0 << k).
v1 = (x << 2*k) ^ (x << k) ^ (x << k) ^ x
// Упрощаем при помощи самоинвертирования (x << k) ^ (x << k) = 0.
v1 = (x << 2*k) ^ xИз этого можно вывести следующее равенство:
Теперь, чтобы алгоритм стал завершённым, нам нужно ещё одно наблюдение: xorshift для k≥w, где w — это ширина целого числа, является no-op. Таким образом, мы многократно применяем удваивающее равенство, пока не достигнем такого достаточно большого q, что xorshift(x,2q⋅k)=x.
Например, чтобы обратить левый xorshift на 13 для 64-битных целых чисел, нам нужно выполнить следующий порядок действий:
Код:
x ^= x << 13 // Девый xorshift на 13.
x ^= x << 13 // Шаг обращения 1.
x ^= x << 26 // Шаг обращения 2.
x ^= x << 52 // Шаг обращения 3.
// x ^= x << 104 // Следующий шаг будет no-op.Вооружившись этим знанием, мы можем приступать к атакам.
Ломаем CityHash64
Давайте взглянем на исходный код CityHash64 (его часть) из libcxx , который используется для хэширования строк на 64-битных платформах:Код стандартной библиотеки C++ подвергается процессу «обезображивания» (uglification), добавляющему перед всеми идентификаторами нижние подчёркивания. Это вызвано тем, что такие идентификаторы зарезервированы стандартом для использования в стандартной библиотеке, а потому не будут заменяться макросами из соблюдающего стандарт кода. Заботясь о вашем душевном здоровье, я убрал их из кода.
Код:
static const uint64_t mul = 0x9ddfea08eb382d69ULL;
static const uint64_t k0 = 0xc3a5c85c97cb3127ULL;
static const uint64_t k1 = 0xb492b66fbe98f273ULL;
static const uint64_t k2 = 0x9ae16a3b2f90404fULL;
static const uint64_t k3 = 0xc949d7c7509e6557ULL;
template<class T>
T loadword(const void* p) {
T r;
std::memcpy(&r, p, sizeof(r));
return r;
}
uint64_t rotate(uint64_t val, int shift) {
if (shift == 0) return val;
return (val >> shift) | (val << (64 - shift));
}
uint64_t hash_len_16(uint64_t u, uint64_t v) {
uint64_t x = u ^ v;
x *= mul;
x ^= x >> 47;
uint64_t y = v ^ x;
y *= mul;
y ^= y >> 47;
y *= mul;
return y;
}
uint64_t hash_len_17_to_32(const char *s, uint64_t len) {
const uint64_t a = loadword<uint64_t>(s) * k1;
const uint64_t b = loadword<uint64_t>(s + 8);
const uint64_t c = loadword<uint64_t>(s + len - 8) * k2;
const uint64_t d = loadword<uint64_t>(s + len - 16) * k0;
return hash_len_16(
rotate(a - b, 43) + rotate(c, 30) + d,
a + rotate(b ^ k3, 20) - c + len
);
}Чтобы поломать этот код, допустим, что мы всегда передаём входные данные длиной 32. Тогда реализация всегда будет вызывать hash_len_17_to_32, а мы будем иметь полный контроль над a, b, c и d при помощи изменения входных данных.
Обратите внимание, что d используется только один раз, в последнем выражении, поэтому становится основной целью для атаки на хэш. Мы выберем a, b и c произвольно, а затем решим уравнение для переменной d, чтобы вычислить желаемый хэш.
При помощи показанной выше функции modinv мы сначала вычисляем нужные обратные по модулю числа для mul и k0:
Код:
>>> 0x9ddfea08eb382d69 * 0xdc56e6f5090b32d9 % 2**64
1
>>> 0xc3a5c85c97cb3127 * 0x81bc9c5aa9c72e97 % 2**64
1Также отметим, что в этом случае xorshift легко обратить, поскольку x ^= x >> 47 является всего лишь обратным самому себе. Подготовив все компоненты, мы можем поэтапно обратить функцию.
Сначала мы загружаем a, b и c, как в хэш-функцию, и вычисляем
Код:
uint64_t v = a + rotate(b ^ k3, 20) - c + len;то есть второй параметр hash_len_16. Затем начиная с нашего желаемого возвращаемого значения hash_len_16(u, v) мы пошагово движемся обратно, обращая каждую операцию для нахождения аргумента функции u, который даст нам целевой hash. Когда мы найдём такое уникальное u, то вычислим требуемое входное d. Соединим всё вместе:
Код:
static const uint64_t mul_inv = 0xdc56e6f5090b32d9ULL;
static const uint64_t k0_inv = 0x81bc9c5aa9c72e97ULL;
void cityhash64_preimage32(uint64_t hash, char *s) {
const uint64_t len = 32;
const uint64_t a = loadword<uint64_t>(s) * k1;
const uint64_t b = loadword<uint64_t>(s + 8);
const uint64_t c = loadword<uint64_t>(s + len - 8) * k2;
uint64_t v = a + rotate(b ^ k3, 20) - c + len;
// Обращаем hash_len_16(u, v). Исходная операция, инвертируемая
// на каждом этапе, показана справа; обратите внимание, что это
// обратный порядок hash_len_16.
uint64_t y = hash; // возвращаем y;
y *= mul_inv; // y *= mul;
y ^= y >> 47; // y ^= y >> 47;
y *= mul_inv; // y *= mul;
uint64_t x = y ^ v; // uint64_t y = v ^ x;
x ^= x >> 47; // x ^= x >> 47;
x *= mul_inv; // x *= mul;
uint64_t u = x ^ v; // uint64_t x = u ^ v;
// Находим loadword<uint64_t>(s + len - 16).
uint64_t d = u - rotate(a - b, 43) - rotate(c, 30);
d *= k0_inv;
std::memcpy(s + len - 16, &d, sizeof(d));
}Вероятность того, что случайное uint64_t образует 8 печатаемых байтов ASCII, равна (94/256)8 ≈ 0,033. Не очень здорово, но cityhash64_preimage32 настолько быстра, что необходимость повторить её примерно три тысячи раз для получения результата из чистого ASCII — это не так уж плохо.
Например, все следующие 10 строк хэшируются в 1337 при использовании CityHash64, сгенерированного при помощи этого кода:
Я заметил, что реальном использовании существуют варианты CityHash64 с незначительными различиями. Я решил атаковать вариант в комплекте libc++, поэтому это должно сработать, например, для её std::hash. Также в статье мы будем рассматривать машину little-endian, на машине big-endian в зависимости от реализации кэша ситуация может быть другой.
Код:
orlp-cityhash64-D-:K5yx*zkgaaaaa
orlp-cityhash64-TXb7;1j&btkaaaaa
orlp-cityhash64-+/LM$0 ;msnaaaaa
orlp-cityhash64-u'f&>I'~mtnaaaaa
orlp-cityhash64-pEEv.LyGcnpaaaaa
orlp-cityhash64-v~~bm@,Vahtaaaaa
orlp-cityhash64-RxHr_&~{miuaaaaa
orlp-cityhash64-is_$34#>uavaaaaa
orlp-cityhash64-$*~l\{S!zoyaaaaa
orlp-cityhash64-W@^5|3^:gtcbaaaaЛомаем MurmurHash2
После атаки на libc++ мы ведь не можем пройти мимо libstdc++? Хэш строк по умолчанию вызывает реализацию MurmurHash2 с seed 0xc70f6907. Хэш, упрощённый так, чтобы обрабатывать строки с длинами, кратными 8, имеет следующий вид:
Код:
uint64_t murmurhash64a(const char* s, size_t len, uint64_t seed) {
const uint64_t mul = 0xc6a4a7935bd1e995ULL;
uint64_t hash = seed ^ (len * mul);
for (const char* p = s; p != s + len; p += 8) {
uint64_t data = loadword<uint64_t>(p);
data *= mul;
data ^= data >> 47;
data *= mul;
hash ^= data;
hash *= mul;
}
hash ^= hash >> 47;
hash *= mul;
hash ^= hash >> 47;
return hash;
}Здесь мы можем использовать ту же методику, что и раньше. Заметим, что обратное по модулю число для 0xc6a4a7935bd1e995 mod 264 — это 0x5f7a0ea7e59b19bd. В качестве примера мы можем выбрать первые 24 байта произвольным образом и найти решение для последних 8 байтов:
Код:
void murmurhash64a_preimage32(uint64_t hash, char* s, uint64_t seed) {
const uint64_t mul = 0xc6a4a7935bd1e995ULL;
const uint64_t mulinv = 0x5f7a0ea7e59b19bdULL;
// Вычисляем состояние хэша для первых 24 байтов обычным образом.
uint64_t state = seed ^ (32 * mul);
for (const char* p = s; p != s + 24; p += 8) {
uint64_t data = loadword<uint64_t>(p);
data *= mul;
data ^= data >> 47;
data *= mul;
state ^= data;
state *= mul;
}
// Обращаем преобразование целевого хэша.
// возвращаем hash;
hash ^= hash >> 47; // hash ^= hash >> 47;
hash *= mulinv; // hash *= mul;
hash ^= hash >> 47; // hash ^= hash >> 47;
// Обращаем последнюю итерацию для последних 8 байтов.
hash *= mulinv; // hash *= mul;
uint64_t data = state ^ hash; // hash = hash ^ data;
data *= mulinv; // data *= mul;
data ^= data >> 47; // data ^= data >> 47;
data *= mulinv; // data *= mul;
std::memcpy(s + 24, &data, 8); // data = loadword<uint64_t>(s);
}Все десять показанных ниже строк хэшируются в этом коде при помощи MurmurHash64A с стандартным seed 0xc70f6907 в 1337:
Код:
orlp-murmurhash64-bhbaaat;SXtgVa
orlp-murmurhash64-bkiaaa&JInaNcZ
orlp-murmurhash64-ewmaaa(%J+jw>j
orlp-murmurhash64-vxpaaag"93\Yj5
orlp-murmurhash64-ehuaaafa`Wp`/|
orlp-murmurhash64-yizaaa1x.zQF6r
orlp-murmurhash64-lpzaaaZphp&c F
orlp-murmurhash64-wsjbaa771rz{z<
orlp-murmurhash64-rnkbaazy4X]p>B
orlp-murmurhash64-aqnbaaZ~OzP_TpУниверсальная коллизионная атака на MurmurHash64A
На самом деле, MurmurHash64A настолько слабый, что Жан-Филип Омассон, Дэниел Бернштайн и Мартин Бослет опубликовали атаку, создающую множества строк, приводящих к коллизиям вне зависимости от использованного случайного seed.Что же касается CityHash64, то для него они тоже нашли универсальные коллизии вне зависимости от используемого seed. На самом деле, CityHash64 поломать таким образом гораздо проще, поскольку простая представленная выше атака нахождения прообраза, нацеленная на 0 в качестве хэша, делает выходные данные полностью зависимыми от seed, а значит, создаёт универсальную коллизию.
Чтобы понять, как это работает, давайте взглянем на основной цикл MurmurHash64A:
Код:
uint64_t data = loadword<uint64_t>(p);
data *= mul; // Тривиально обратимо.
data ^= data >> 47; // Тривиально обратимо.
data *= mul; // Тривиально обратимо.
state ^= data;
state *= mul;Мы знаем, что тривиальным образом можем обратить выполняемые с data операции вне зависимости от текущего состояния, поэтому вполне могли бы иметь следующее тело:
Код:
state ^= data;
state *= mul;Теперь хэш и в самом деле начинает выглядеть довольно слабо. Авторы исследования использовали хитрый трюк: создавали одновременно две строки так, чтобы они отличались ровно на старший бит в каждом 8-байтном слове. Почему на старший бит?
Код:
>>> 1 << 63
9223372036854775808
>>> (1 << 63) * mul % 2**64
9223372036854775808Так как mul нечётное, самый младший бит установлен. Умножение 1 << 63 на него эквивалентно сдвигу этого бита на 63 позиций влево, что снова будет равно 1 << 63. То есть 1 << 63 — это фиксированная точка для операции state *= mul. Также стоит отметить, что XOR старшего бита эквивалентно сложению, поскольку переполнение от сложения убирается mod 264.
То есть если у нас есть две входные строки: одна, начинающаяся с 8-байтных data, а другая, начинающаяся с data ^ (1 << 63) == data + (1 << 63) (после выполнения тривиальных инверсий) — то мы выясним, что два состояния вне зависимости от seed различаются ровно на старший бит после state ^= data. После умножения мы обнаружим, что два состояния имеют вид x * mul и (x + (1 << 63)) * mul == x * mul + (1 << 63)… то есть снова различаются ровно на верхний бит! Теперь мы вернулись для следующих 8 байтов к state ^= data в нашей итерации. Можно воспользоваться этим моментом для отмены разницы в старшем бите, снова передав две 8-байтные строки, отличающиеся на старший бит (после обращения).
На самом деле, нам достаточно найти только одну пару таких строк, отличающихся на старший бит, которую мы затем можем повторить дважды (в любом порядке), чтобы снова отменить разницу. Если данные представлены в виде uint64_t, то когда мы выберем первую строку как x, сможем получить вторую строку как
Код:
x *= mul; // Преобразование вперёд...
x ^= x >> 47; // ...
x *= mul; // ...
x ^= 1 << 63; // Разница в старшем бите.
x *= mulinv; // Преобразование назад...
x ^= x >> 47; // ...
x *= mulinv; // ...Мне не удалось найти печатаемую строку ASCII, которая бы имела в качестве пары другую печатаемую строку ASCII. Но я нашёл следующую пару 8-байтных строк UTF-8, после преобразования входных данных Murmurhash64A отличающуюся ровно на верхний бит:
Код:
xx0rlpx!
xxsXъВСкомбинировав их, мы получим две 16-байтные строки, которые при обработке алгоритмом хэширования позволяют манипулировать состоянием аналогичным образом: создавая коллизию.
Код:
xx0rlpx!xxsXъВ
xxsXъВxx0rlpx!Но на этом всё не заканчивается. Выполнив конкатенацию этих двух строк, мы можем создать 2n различных строк с коллизиями, каждая из которых имеет длину 16n. При текущей реализации libstdc++ показанный ниже код выведет восемь раз одно и то же число:
Код:
std::hash<std::u8string> h;
std::u8string a = u8"xx0rlpx!xxsXъВ";
std::u8string b = u8"xxsXъВxx0rlpx!";
std::cout << h(a + a + a) << "\n";
std::cout << h(a + a + b) << "\n";
std::cout << h(a + b + a) << "\n";
std::cout << h(a + b + b) << "\n";
std::cout << h(b + a + a) << "\n";
std::cout << h(b + a + b) << "\n";
std::cout << h(b + b + a) << "\n";
std::cout << h(b + b + b) << "\n";Даже если бы libstdc++ рандомизировала seed, используемый MurmurHash64a, коллизии строк всё равно бы происходили.
Ломаем MurmurHash3
NimПока я прокрастинировал, заканчивая эту статью, Nim перешёл на использование farmhash. Сделайте вид, что он всё ещё использует MurmurHash3, чтобы мои слова имели смысл. А потом я поломаю и farmhash.
Если мы снова упростим и будем учитывать только строки, длина которых кратна 4, то получим следующий код:
Код:
uint32_t rotl32(uint32_t x, int r) {
return (x << r) | (x >> (32 - r));
}
uint32_t murmurhash3_x86_32(const char* s, int len, uint32_t seed) {
const uint32_t c1 = 0xcc9e2d51;
const uint32_t c2 = 0x1b873593;
const uint32_t c3 = 0x85ebca6b;
const uint32_t c4 = 0xc2b2ae35;
uint32_t h = seed;
for (const char* p = s; p != s + len; p += 4) {
uint32_t k = loadword<uint32_t>(p);
k *= c1;
k = rotl32(k, 15);
k *= c2;
h ^= k;
h = rotl32(h, 13);
h = h * 5 + 0xe6546b64;
}
h ^= len;
h ^= h >> 16;
h *= c3;
h ^= h >> 13;
h *= c4;
h ^= h >> 16;
return h;
}Думаю, теперь вы уже должны понимать, как заставить эту функцию выдавать любые значения, если знаете seed. Инверсией rotl32(x, r) будет rotl32(x, 32-r), а инверсией h ^= h >> 16 снова будет просто h ^= h >> 16. Только с h ^= h >> 13 ситуация немного отличается: мы впервые видим здесь, что инверсия xorshift требует больше, чем один шаг:
Код:
h ^= h >> 13
h ^= h >> 26Вычислим обратные по модулю числа для значений с c1 по c4, а также 5 mod 232. Если вы хотите сжульничать или проверить свой ответ, то можете заглянуть в код , который я использовал для генерации следующих десяти строк, которые при передаче MurmurHash3_x86_32 с seed 0 все хэшируются в 1337:
Код:
orlp-murmurhash3_x86_32-haaaPa*+
orlp-murmurhash3_x86_32-saaaUW&<
orlp-murmurhash3_x86_32-ubaa/!/"
orlp-murmurhash3_x86_32-weaare]]
orlp-murmurhash3_x86_32-chaa5@/}
orlp-murmurhash3_x86_32-claaM[,5
orlp-murmurhash3_x86_32-fraaIx`N
orlp-murmurhash3_x86_32-iwaara&<
orlp-murmurhash3_x86_32-zwaa]>zd
orlp-murmurhash3_x86_32-zbbaW-5GNim использует в качестве фиксированного seed 0.
Вы можете задаться вопросом этичности публикации функций для генерации произвольного количества коллизий для хэш-функций, которые продолжают использоваться сегодня. Но атака HashDoS известна уже почти два десятка лет, а показанные мной универсальные коллизии хэшей, тоже были опубликованы больше десятка лет назад. У всех желающих было достаточно времени, чтобы всё исправить.
Атака универсальными коллизиями на MurmurHash3
Предположим, что Nim не использовал бы 0 в качестве фиксированного seed, а выбрал случайно сгенерированный. Можем ли мы провести атаку, похожую на атаку MurmurHash2, чтобы тоже генерировать универсальные множественные коллизии?Да, можем. Давайте ещё раз взглянем на тело основного цикла:
Код:
uint32_t k = loadword<uint32_t>(p);
k *= c1; // Тривиально обратимо.
k = rotl32(k, 15); // Тривиально обратимо.
k *= c2; // Тривиально обратимо.
h ^= k;
h = rotl32(h, 13);
h = h * 5 + 0xe6546b64;Можно снова игнорировать первые три тривиально обратимые команды, потому что мы можем просто выбрать входные данные так, чтобы получить нужное нам k. Вспомним из предыдущего примера, что мы хотим добавить разницу только в старший бит h, так как при умножении эта разница сохранится. Но между XOR и умножением присутствует циклический битовый сдвиг. Как же решить эту проблему? Просто вставить нашу разницу битов так, чтобы rotl32(h, 13) сдвигал её в старшую позицию.
Помешает ли нам прибавление 0xe6546b64? Нет. Поскольку между двумя состояниями различается только старший бит, между двумя состояниями существует разность, равная 231. Эта разность сохраняется при сложении. Так как два 32-битных числа с одинаковым старшим битом могут быть иметь расстояние между друг другом не более 231−1, можно сделать вывод, что после сложения два состояния по-прежнему будут различаться в старшем бите.
То есть мы хотим найти две пары 32-битных int, такие, что после применения первых трёх команд первая пара будет отличаться в бите 1 << (31 - 13) == 0x00040000, а вторая — в бите 1 << 31 == 0x80000000.
После поиска перебором я нашёл несколько хороших пар (мне снова пришлось использовать UTF-8), которые при комбинировании дали мне следующую коллизию:
Код:
a = "!&orlpՓ"
b = "yǏglp$X"Как и раньше, любая конкатенация строк a и b длиной n образует коллизию со всеми комбинациями длиной n.
Ломаем FarmHash64
После того, как я начал писать этот пост, Nim перешёл на farmhash. Чтобы поломать его, можно воспользоваться наблюдением, что его структура очень похожа на CityHash64, поэтому мы можем снова применить те же приёмы. На самом деле, единственные изменения между ними для длин в 17-32 байта заключаются в том, что некоторые операторы были заменены с вычитания/XOR на сложение, была изменена константа оператора циклического сдвига, а также немного изменён способ использования констант k. Процесс его взлома настолько схож, что полностью аналогичен, поэтому можно сразу перейти к результату. Эти десять строк хэшируются при помощи FarmHash64 в 1337:
Код:
orlp-farmhash64-?VrJ@L7ytzwheaaa
orlp-farmhash64-p3`!SQb}fmxheaaa
orlp-farmhash64-pdt'cuI\gvxheaaa
orlp-farmhash64-IbY`xAG&ibkieaaa
orlp-farmhash64-[_LU!d1hwmkieaaa
orlp-farmhash64-QiY!clz]bttieaaa
orlp-farmhash64-&?J3rZ_8gsuieaaa
orlp-farmhash64-LOBWtm5Szyuieaaa
orlp-farmhash64-Mptaa^g^ytvieaaa
orlp-farmhash64-B?&l::hxqmfjeaaaТривиальные множественные коллизии wyhash с фиксированным seed
Zig использует wyhash с фиксированным seed 0. Хоть я не смог выполнить независимые от seed атаки на wyhash, его использование с фиксированным seed делает генерацию коллизий тривиальной. Wyhash основан на folded multiply, которое получает на входе два 64-битных значения, умножает их, получая 128-битное произведение, а затем выполняет XOR двух половин:
Код:
uint64_t folded_multiply(uint64_t a, uint64_t b) {
__uint128_t full = __uint128_t(a) * __uint128_t(b);
return uint64_t(full) ^ uint64_t(full >> 64);
}Для протокола: это не претензия к wyhash в целом. Он кажется надёжным, если используется с секретным рандомизированным seed. Я просто хочу показать, что если использовать его с фиксированным seed, то он тривиально ломается.
Здесь можно легко увидеть критичный недостаток: если одна из половин равна нулю, то результатом тоже будет ноль. Чтобы защититься от этого, wyhash всегда использует folded multiply в следующем виде:
Код:
out = folded_multiply(input_a ^ secret_a, input_b ^ secret_b);где secret_a и secret_b определяются по seed или по выходным данным предыдущих итераций, на которые влиял seed. Однако когда seed константа… Применив немного изобретательности , мы можем использовать начало нашей строки для подготовки «секретного» значения, которое мы можем прекрасно обнулить с другой строкой ASCII в дальнейшем во входных данных.
Итак, без лишних предисловий скажем, что каждая 32-битная строка вида
Код:
orlp-wyhash-oGf_________tWJbzMJRхэшируется хэшером Zig по умолчанию в одно и то же значение.
Zig использует набор параметров, отличающийся от значений по умолчанию из репозитория wyhash, поэтому надо добавить, что этот паттерн обеспечивает произвольные множественные коллизии для параметров по умолчанию, найденных в wyhash, и при использовании seed == 0:
Код:
orlp-wyhash-EUv_________NLXyytkpЗаключение
Как мы увидели, многие хэш-функции, активно используемые сегодня в хэш-таблицах, очень слабы. Они позволяют выполнять достаточно тривиальные атаки, приводящие к созданию произвольных количеств коллизий в случае отсутствия случайной инициализации. Использование хэш-таблицы со случайным seed — дело первостепенной важности, если вы не хотите стать жертвой атаки hash flooding.Также мы увидели, что некоторые хэш-функции уязвимы к атаке даже при случайных seed. Они полностью сломаны и их нельзя использовать, если существует хотя б минимальная возможность атаки. К счастью, мне не удалось найти такие атаки против большинства хэшей, но возможность ее существования пугает.
При использовании универсального хэширования можно создать хэш-функции, но такая атака доказуемо невозможна: в прошлом году я опубликовал хэш-функцию polymur-hash, обладающую таким свойством. Кроме того, ваше HTTPS-подключение к моему веб-сайту, скорее всего, использует универсальную хэш-функцию для обеспечения подлинности передаваемых данных: и Poly1305, и GCM основаны на универсальном хэшировании для доказательства их безопасности.
Примечание: доказано, что такие атаки невозможны для неинтерактивных нападающих, но всё снова идёт прахом, если нападающий может изучать выходные хэши и использовать их, чтобы попытаться угадать ваш секретный ключ.
Разумеется, если ваши данные не контролируются пользователем или если отсутствует разумная модель безопасности в тех местах, где ваше приложение может подвергаться атакам, то вы можете обойтись более быстрыми и небезопасными хэшами.
